Compute 95% Credible Interval and Mean

Small helper function that computes the 2.5% and 97.5% quantiles and the mean of a vector. Useful for example when using function predict.bamlss.

c95(x)

Arguments

x

A numeric vector.

Examples

x <- rnorm(100)
c95(x)
#>        2.5%        Mean       97.5% 
#> -2.03558585 -0.08520532  1.96359896 

if (FALSE) ## Example computing predictions.
set.seed(123)
d <- data.frame("x" = seq(-3, 3, length = 30))
d$y <- sin(d$x) + rnorm(30, sd = 0.3)

## Estimate model and compute predictions.
## with c95().
b <- bamlss(y ~ s(x), data = d)
#> AICc  32.4494 logPost -45.4219 logLik  -9.3006 edf 5.4381 eps 0.5421 iteration   1
#> AICc  20.6556 logPost -37.4143 logLik  -3.1010 edf 5.6297 eps 0.1766 iteration   2
#> AICc  15.6084 logPost -34.5604 logLik   0.1807 edf 6.0962 eps 0.1383 iteration   3
#> AICc  14.6331 logPost -34.0098 logLik   1.2677 edf 6.4519 eps 0.0783 iteration   4
#> AICc  14.5393 logPost -33.9662 logLik   1.6215 edf 6.6299 eps 0.0344 iteration   5
#> AICc  14.5353 logPost -33.9652 logLik   1.7003 edf 6.6740 eps 0.0081 iteration   6
#> AICc  14.5352 logPost -33.9653 logLik   1.7114 edf 6.6803 eps 0.0011 iteration   7
#> AICc  14.5352 logPost -33.9653 logLik   1.7127 edf 6.6810 eps 0.0001 iteration   8
#> AICc  14.5352 logPost -33.9653 logLik   1.7129 edf 6.6811 eps 0.0000 iteration   9
#> AICc  14.5352 logPost -33.9653 logLik   1.7129 edf 6.6811 eps 0.0000 iteration   9
#> elapsed time:  0.06sec
#> Starting the sampler...
#> 
#> |                    |   0%  0.95sec
#> |*                   |   5%  0.89sec  0.05sec
#> |**                  |  10%  0.84sec  0.09sec
#> |***                 |  15%  0.84sec  0.15sec
#> |****                |  20%  0.81sec  0.20sec
#> |*****               |  25%  0.77sec  0.26sec
#> |******              |  30%  0.75sec  0.32sec
#> |*******             |  35%  0.70sec  0.38sec
#> |********            |  40%  0.66sec  0.44sec
#> |*********           |  45%  0.60sec  0.49sec
#> |**********          |  50%  0.55sec  0.55sec
#> |***********         |  55%  0.50sec  0.61sec
#> |************        |  60%  0.44sec  0.66sec
#> |*************       |  65%  0.39sec  0.72sec
#> |**************      |  70%  0.33sec  0.78sec
#> |***************     |  75%  0.28sec  0.84sec
#> |****************    |  80%  0.22sec  0.90sec
#> |*****************   |  85%  0.17sec  0.97sec
#> |******************  |  90%  0.11sec  1.03sec
#> |******************* |  95%  0.06sec  1.08sec
#> |********************| 100%  0.00sec  1.13sec
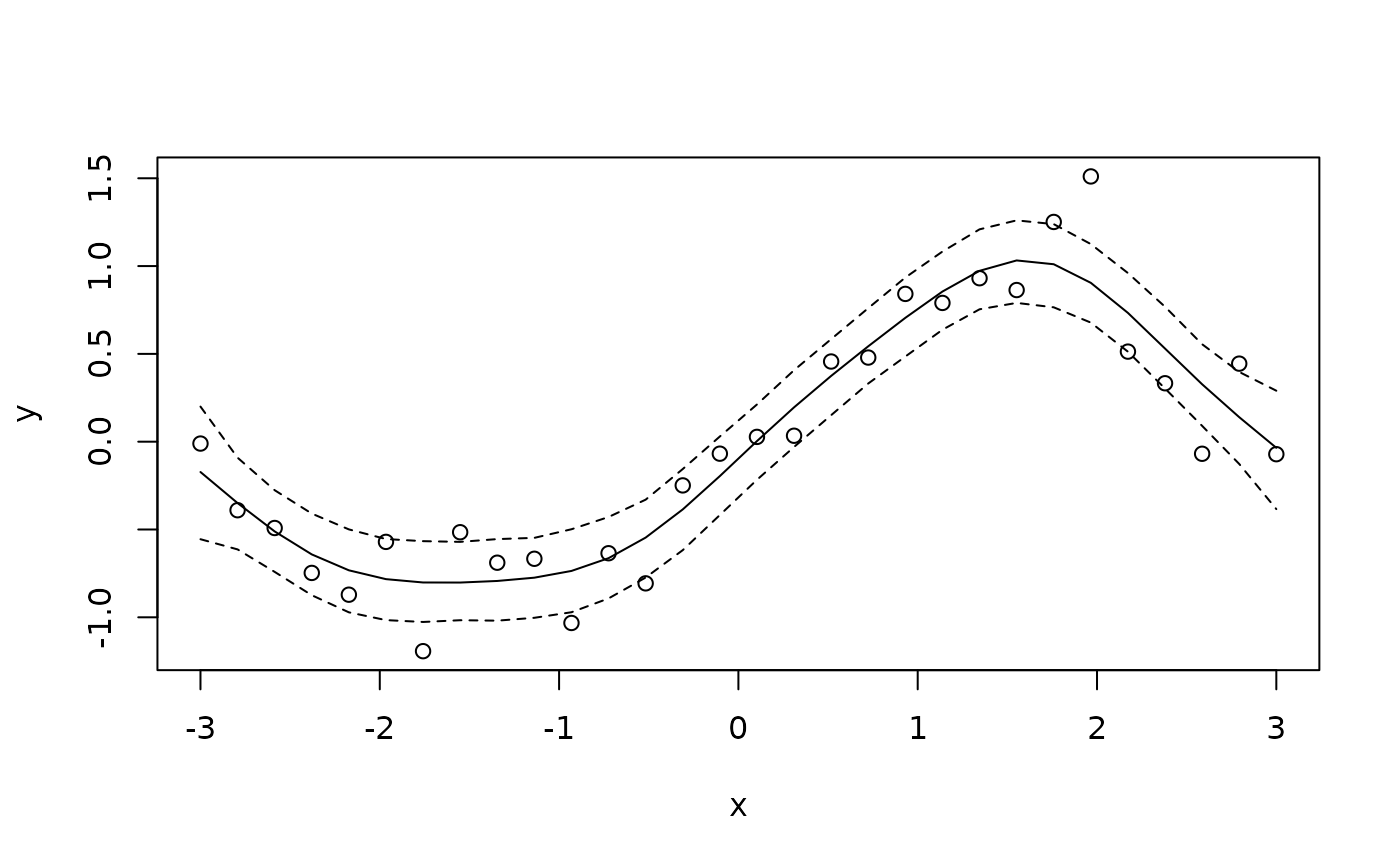
p <- predict(b, model = "mu", FUN = c95)
plot(d)
matplot(d$x, p, type = "l", lty = c(2, 1, 2),
  col = "black", add = TRUE)


## Example extracting coefficients.
coef(b, FUN = c95)
#>                           2.5%        Mean       97.5%
#> mu.s.s(x).b1        -2.7128249 -2.07000703 -1.44983517
#> mu.s.s(x).b2        -1.4800066  0.31732825  2.23923359
#> mu.s.s(x).b3        -0.6976676 -0.17336785  0.35867711
#> mu.s.s(x).b4        -1.2198943  0.15481990  1.54778071
#> mu.s.s(x).b5        -0.4754548  0.05119379  0.52651786
#> mu.s.s(x).b6        -1.5442848 -0.17577973  1.04634256
#> mu.s.s(x).b7        -0.6296562 -0.05705302  0.40215896
#> mu.s.s(x).b8        -2.9576602 -0.04595215  2.79233488
#> mu.s.s(x).b9        -2.5895736 -1.51987111 -0.34548875
#> mu.s.s(x).tau21      2.8397411 13.59739370 48.98173816
#> mu.s.s(x).alpha      1.0000000  1.00000000  1.00000000
#> mu.p.(Intercept)    -0.1202318 -0.01986826  0.06927125
#> mu.p.alpha           1.0000000  1.00000000  1.00000000
#> sigma.p.(Intercept) -1.6712943 -1.39173221 -1.09268439
#> sigma.p.alpha        0.5042547  0.93969229  1.00000000