Bayesian Multinomial Regression • bamlss

This vignette is based on Yee (2010). The data is about the marital status of white male in New Zealand in the early 1990s. The aim of this analysis is to explore how the marital status varies with age. The data can be loaded with

data("marital.nz", package = "VGAM")
head(marital.nz)

##   age ethnicity            mstatus
## 1  29  European             Single
## 2  55  European  Married/Partnered
## 3  44  European  Married/Partnered
## 4  53  European Divorced/Separated
## 5  45  European  Married/Partnered
## 7  30  European             Single

levels(marital.nz$mstatus)

## [1] "Divorced/Separated" "Married/Partnered"  "Single"            
## [4] "Widowed"

The response mstatus has 4 levels. We use a multinomial logit model to estimate the age effect, therefore, one category needs to be specified as a reference category. The model can be estimated with

## Model formula, each category may
## have different model terms.
f <- list(
  mstatus ~ s(age),
          ~ s(age),
          ~ s(age)
)

## Set the seed for reproducibility.
set.seed(123)

## Estimate.
b <- bamlss(f, family = "multinomial", data = marital.nz,
  reference = "Married/Partnered")

The model summary gives

summary(b)

## 
## Call:
## bamlss(formula = f, family = "multinomial", data = marital.nz, 
##     reference = "Married/Partnered")
## ---
## Family: multinomial 
## Link function: DivorcedSeparated = log, Single = log, Widowed = log
## *---
## Formula DivorcedSeparated:
## ---
## DivorcedSeparated ~ s(age)
## -
## Parametric coefficients:
##               Mean   2.5%    50%  97.5% parameters
## (Intercept) -2.678 -2.810 -2.677 -2.553     -2.673
## -
## Acceptance probability:
##         Mean   2.5%    50% 97.5%
## alpha 0.9775 0.7937 0.9999     1
## -
## Smooth terms:
##                   Mean      2.5%       50%     97.5% parameters
## s(age).tau21 3.454e+00 3.415e-04 1.359e+00 2.122e+01      0.760
## s(age).alpha 8.921e-01 2.488e-01 9.882e-01 1.000e+00         NA
## s(age).edf   2.883e+00 1.003e+00 2.834e+00 5.178e+00      2.471
## ---
## Formula Single:
## ---
## Single ~ s(age)
## -
## Parametric coefficients:
##               Mean   2.5%    50%  97.5% parameters
## (Intercept) -2.498 -2.622 -2.498 -2.371     -2.483
## -
## Acceptance probability:
##         Mean   2.5%    50% 97.5%
## alpha 0.9893 0.9060 1.0000     1
## -
## Smooth terms:
##                   Mean      2.5%       50%     97.5% parameters
## s(age).tau21  50.13453  10.49526  36.35219 172.98182     38.128
## s(age).alpha   0.69769   0.01797   0.83127   1.00000         NA
## s(age).edf     6.14119   4.89753   6.10817   7.61407      6.153
## ---
## Formula Widowed:
## ---
## Widowed ~ s(age)
## -
## Parametric coefficients:
##               Mean   2.5%    50%  97.5% parameters
## (Intercept) -5.021 -5.418 -5.015 -4.639     -5.007
## -
## Acceptance probability:
##         Mean   2.5%    50% 97.5%
## alpha 0.9676 0.7179 1.0000     1
## -
## Smooth terms:
##                   Mean      2.5%       50%     97.5% parameters
## s(age).tau21 1.104e+00 9.176e-05 1.774e-02 1.187e+01      0.000
## s(age).alpha 9.515e-01 6.050e-01 9.993e-01 1.000e+00         NA
## s(age).edf   1.358e+00 9.999e-01 1.052e+00 3.758e+00      0.999
## ---
## Sampler summary:
## -
## DIC = 6548.918 logLik = -3266.961 pd = 14.9952
## runtime = 23.48
## ---
## Optimizer summary:
## -
## AICc = 6545.31 edf = 12.6224 logLik = -3260.004
## logPost = -3282.925 nobs = 6053 runtime = 3.083

and suggests reasonable acceptance rates. However, for a final model run it is recommend to increase the number of iteration, the burn-in phase as well as the thinning parameter of the sampling engine function sam_GMCMC(). The estimated effects can be plotted with

par(mfrow = c(1, 3), mar = c(4.1, 4.1, 0.1, 1.1))
plot(b)

To calculate estimated age dependent probabilities for each category, we use the predict.bamlss() method.

## Create a data frame for prediction.
nd <- data.frame("age" = seq(20, 90, length = 100))

## Predict for the three levels.
p <- predict(b, newdata = nd, type = "parameter")

Now, note that the specification of the predictors in the multinomial_bamlss() family is based on a logarithmic link, therefore, to compute the probabilities we run the following code:

probs <- list()
for(j in names(p))
  probs[[j]] <- p[[j]] / (1 + rowSums(do.call("cbind", p)))
probs <- as.data.frame(probs)
probs[["MarriedPartnered"]] <- 1 - rowSums(probs)

The estimated probabilities can then be visualized with:

par(mar = c(4.1, 4.1, 1.1, 1.1))
plot2d(probs ~ age, data = nd, col.lines = rainbow_hcl(4),
  lwd = 2, scheme = 1, ylab = "Fitted probabilities", ylim = c(0, 1))
legend("center", names(probs), lty = 1, lwd = 2, col = rainbow_hcl(4))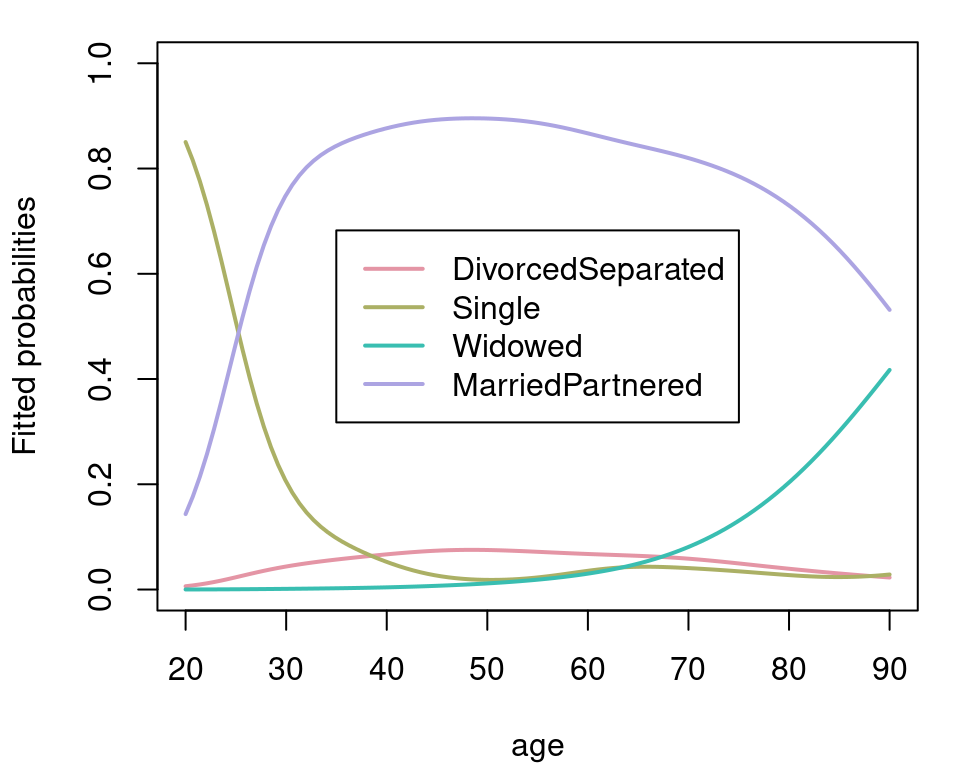

References

Umlauf, Nikolaus, Nadja Klein, Achim Zeileis, and Thorsten Simon. 2024. bamlss: Bayesian Additive Models for Location Scale and Shape (and Beyond). https://CRAN.R-project.org/package=bamlss.

Yee, Thomas W. 2010. “The VGAM Package for Categorical Data Analysis.” Journal of Statistical Software 32 (10): 1–34. https://doi.org/10.18637/jss.v032.i10.